Addition Of Vectors (Graphical Method)

Two vectors can be added if both of them are of the same nature.

Example:- A displacement vector cannot be added to a force but can we added to displacement vector only.

The graphical method of addition of vectors are as under.

1. Triangle Law Of Vector Addition

This law state that “If two vectors can be represented both in magnitude and direction by the two sides of a triangle taken in the same order, then their resultant is represented completely, both in magnitude and direction by the third side of the triangle taken in opposite order”.

Let two vector A and B that lie in a plane. We draw a vector OM, equal and parallel to vector A and from head of OM, we draw a vector MN equal and parallel to vector B. Then the resultant vector is given by ON, which joins the tail of A and head of B.

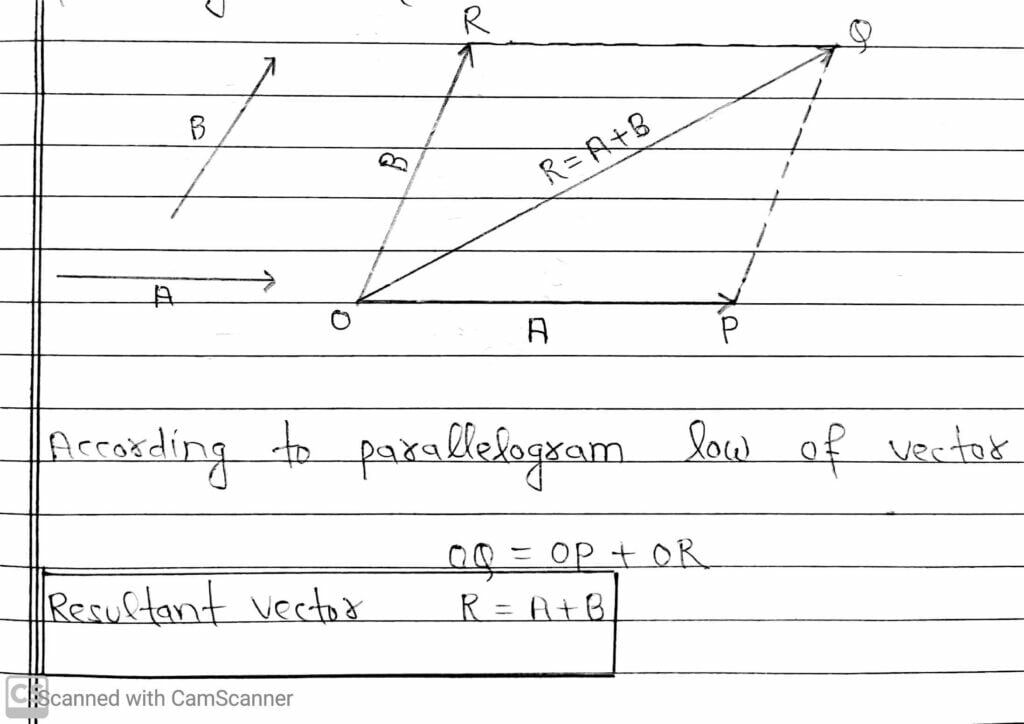
2. Parallelogram Law Of Vector Addition

This law state that “If two vectors can be represented both in magnitude and direction by the two adjacent sides of a parallelogram drawn from a common point, then their resultant is completely represented both in magnitude and direction by the diagonal of the parallelogram drawn from that point”.

Let two vectors A and B that lie in a plane. From a common point O, we draw a vector OP equal and parallel to A and vector OR equal and parallel to B. Now, we complete a parallelogram OPQR.

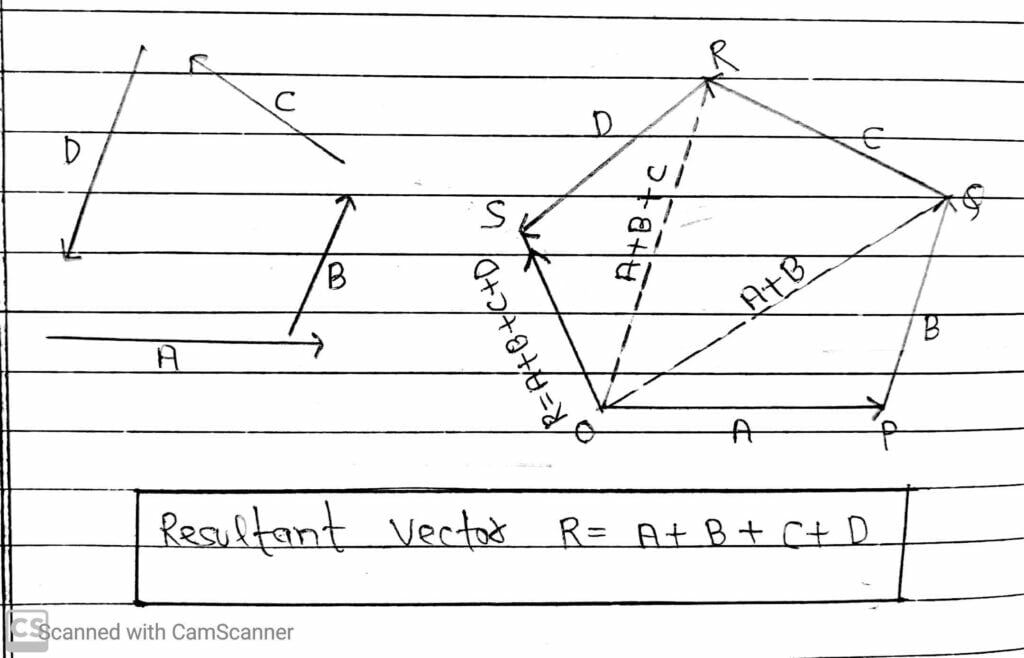
3. Polygon Law Of Vector Addition

This law state that “When a number of vectors are represented in both magnitude and direction by the sides of an open polygon taken in an order, then their resultant is represented in both magnitude and direction by the closing side of the polygon taken in opposite order”.

Subtraction Of Two Vectors (Graphical Method)

If a vector B is to be subtracted from vector A, then we have to invert the vector B and then add it with vector A according to laws of addition of two vectors.

Hence, the subtraction of vector B from a vector A is defined as the addition of vector (-B) to vector A.

Subtraction Of Two Vectors (Graphical Method)

NCERT Class 11 Physics Book PDF Free Download

1. Triangle Law Of Vector Addition

2. Parallelogram Law Of Vector Addition

3. Polygon Law Of Vector Addition

Subtraction Of Two Vectors (Graphical Method)

Also Read

NCERT Class 11 Physics Hand Written Notes Chapter-Wise

Related