Dimensional Analysis And It's Applications » Maths And Physics With Pandey Sir

The dimensional analysis helps us in reducing the relations among different physical quantities and checking the accuracy, derivation and dimensional consistency or its homogeneity of various numerical expressions.

It’s applications are as given below

1. Checking The Dimensional Consistency Of Equations

To check the dimensional correctness of a physical equation. For this purpose we make use of the principal of homogeneity of dimensions.

” The principle of homogeneity of dimension state that a physical quantity equation will be dimensionally correct, if the dimensions of all the terms occurring on both side of the equation are same.

Example:- The equation of motion s = ut+1/2×at. Dimension of different terms are-

[S] = [L]

[ut] = [LT⁻¹] [T] = [L]

[1/2×at²] = [LT⁻²] [T²] = [L]

All the terms on both side of the equation have the same dimensions, So the given equation is dimensionally correct.

2. Conversion Of One System Of Units Into Another

It is based on the fact that the magnitude of a physical quantity remains the same whatever may be the System of units. Let u₁ and u₂ are the units of measurement of a physical quantity Q and n₁ and n₂ are the corresponding numerical values, then

Q = n₁u₁ = n₂u₂ – (I)

Let M₁, L₁ and T₁ be the sizes of fundamental units of mass, length and time in one system; and M₂, L₂ and T₂ be corresponding units in another system.

Conversion of one system of units into another

This equation can be used to find the numerical value in the second of new system of unit.

Example:- Let us convert 1 joule into erg Dimensional formula of energy is [ML²T⁻²]

Therefore a=1, b=2, c=-2

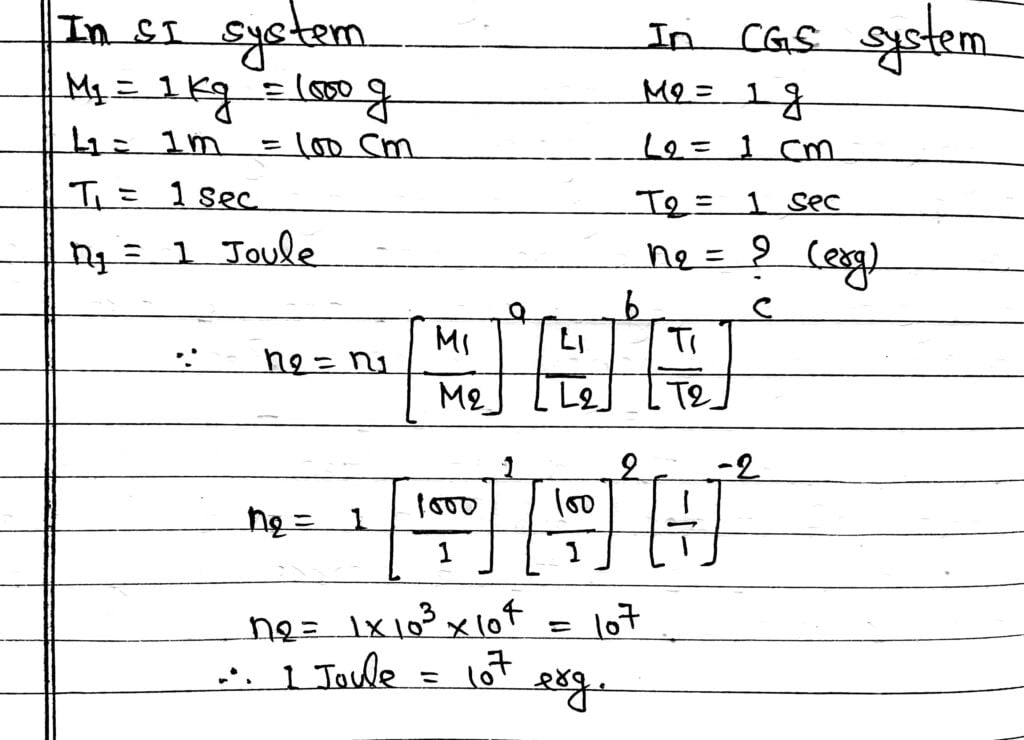
3. Deducing Relation Among The Physical Quantity

By making use of the homogeneity of dimensions, we can derive an expression for a physical quantity, if we know the various factors on which it depends.

Let us derive an expression for the centripetal force F acting on a particle of mass m moving with velocity v in a circle of radius r.