All matter is made up of molecules. The molecules of a gas are in state of rapid and continuous motion. Their velocity depends on temperature.
Using this molecular motion, various properties of a gas like pressure, temperature, energy etc, can be explained. Hence this theory is called kinetic theory of gases which was developed by Claussius, Maxwell and Ludwig Boltzmann.
Assumptions Of Kinetic Theory Of Gases
(I) A given amount of gas consists of a very large number of molecules (of the order of Avogadro numbers 10²³) and all molecules are identical in all respect.
(II) The molecules of a gas are in a state of incessant random motion in all direction with different speeds, move freely in straight line following Newton’s first law.
(III) The size of molecule is much smaller than the average separation between the molecules. At ordinary pressure and temperature, the average distance between molecules is about 20 angstrom, where as size of molecules is 2 angstrom.
(IV) There is no intermolecular force between molecules of gas except during collision.
(V) The collision between molecules among themselves or between molecules and walls are perfectly elastic.
(VI) The duration of collision between two molecules is negligible as compared to the time interval of two successive collisions.
(VII) The density and the distribution of molecules is uniform throughout the gas.
Pressure Of An Ideal Gas
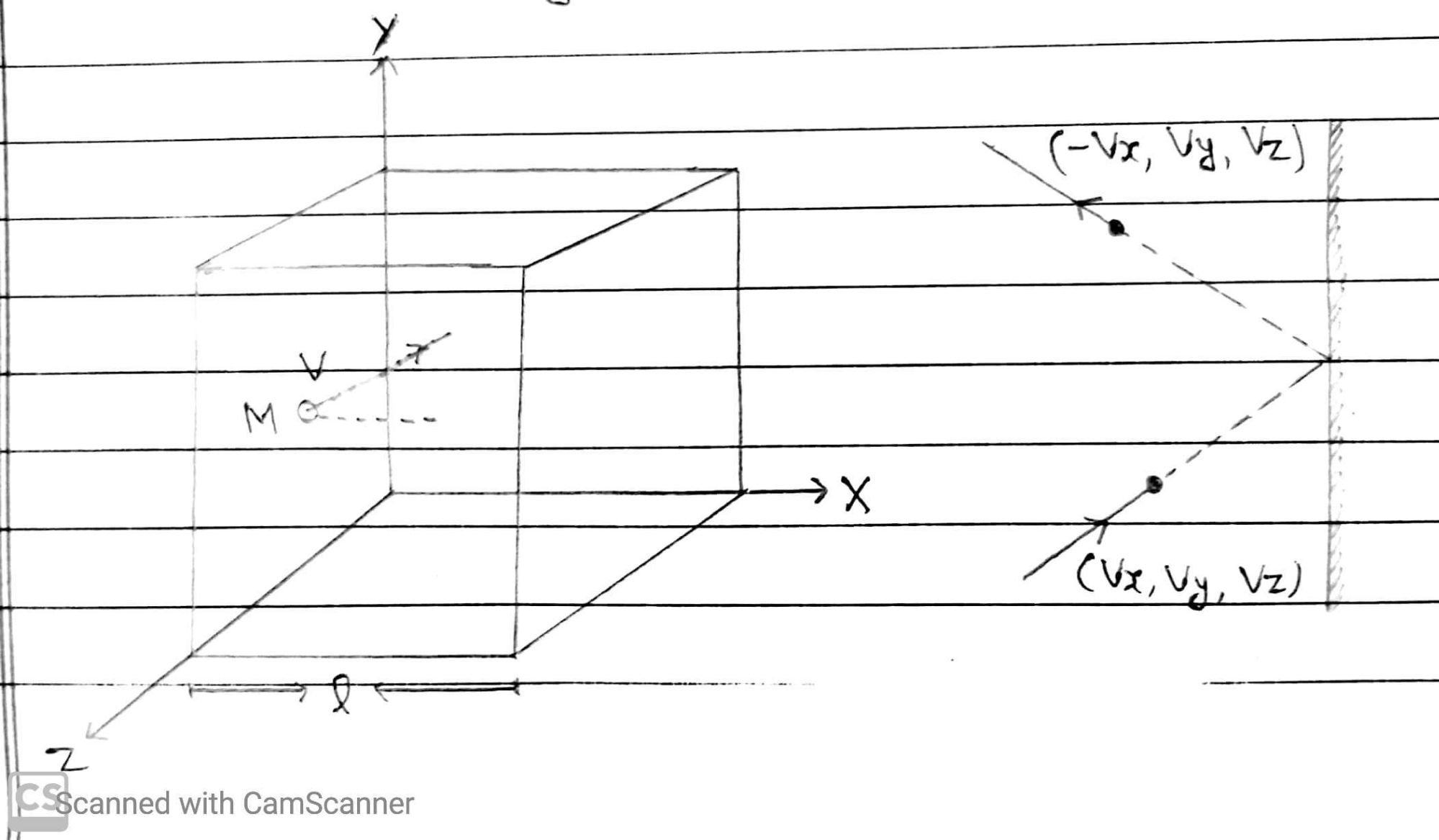
Let an ideal gas containing of N molecules in a container of volume V. The container is a cube with edges of length l. Let a molecules of mass m moving with velocity Vx, Vy and Vz along X, Y and Z Axis.
As molecules collides with the wall parallel to YZ- Plane elasticly. it’s x component of velocity is reversed, while its y and z component of velocity remains unaltered.
So, velocity after collision along X,Y and Z Axis are (-Vx, Vy and Vz).
Relation Between Pressure Exerted By An Ideal Gas and It’s Density
Let M be the mass of all molecules of a given ideal gas enclosed in a vessel of volume V having density ρ, then

Kinetic Interpretation Of Temperature
The average kinetic energy of a molecule depends on the absolute Temperature of the gas. It is the Kinetic interpretation of temperature.
Let us consider a sample of an ideal gas having N number of molecules. Let the volume of the gas is V, pressure is P and temperature is T.


It is clear that average kinetic energy of a molecule is directly proportional to the absolute Temperature of the gas.
It is independent of pressure, volume and the nature of the ideal gas.
Root Mean Square Speed
The square root of the mean square speed V⁻² is known as root mean square speed.

Maxwell’s Speed Distribution
In any gas, the molecules randomly collide against each other. So the velocity of any individual gas molecules changes continuously. At any instant the speed of the molecules vary over a wide range. However, the velocities distribution remains fixed in a steady state. James Clerk Maxwell was the first to derive a mathematical relation for the most probable distribution of speeds among the molecules of a gas.






