Periodic Motion
Any motion that repeats itself over and over again at regular intervals of time is called periodic or harmonic motion.
Example: (I) The motion of any planet around the sun in an elliptical orbit is periodic.
(II) The motion of the moon around the earth is periodic.
(III) The motion of the hands of a clock is periodic.
Oscillatory Motion
If a body moves back and forth repeatedly about its mean position, its motion is said to be oscillatory or vibratory or harmonic motion. Such a motion repeats itself over and over again about a mean position such that it remains confined within well defined limits (known as extreme position) on either side of the mean position.
Example: (I) The swinging motion of the pendulum of a wall clock.
(II) The vibrations of the string of a guitar.
(III) The motion of the piston of an automobile engine.
(IV) The oscillations of a mass suspended from a spring.
Periodic Motion Vs Oscillatory Motion
Every oscillatory motion is necessary periodic because it is repeated at regular intervals of time. In addition, it is bounded about one mean position. But every periodic motion need not to be oscillatory.
For example the earth complete one revolution around the sun in one year, but it is not a to and fro motion about any mean position. Hence, its motion is periodic but not oscillatory.
Period and Frequency
Period
The smallest interval of time after which a periodic motion is repeated is called its period.
It’s SI unit is second and denoted by T. Period of oscillations should have a very high range of accuracy. So its unit varies with the necessity.
Example: (I) Period of revolution of the planet Mercury is 88 Earth day.
(II) Period of vibration of a quartz crystal is expressed in units of microsecond(10⁻⁶ s) = 1μs
Frequency
The number of oscillations/vibrations performed by oscillatory body about its mean position in a unit time is known as its frequency.
The SI unit of frequency is Hertz(Hz) on the name of the Heinrich Rudolph Hertz (1857-1894) who discovered radio wave.
Frequency can also be defined as reciprocal of time period. It is denoted by f or v.
Frequency, f = 1/T
Displacement
In oscillations, we use term displacement as the change in position with respect to mean position or equilibrium position or reference position.
Displacement Of a Particle
(I) Let a block is attached to a spring at one of its end, the other end of which is fixed to a rigid wall. Generally, it is convenient to measure the displacement variables (x) as the deviation of the block from the mean position of the oscillation with time.

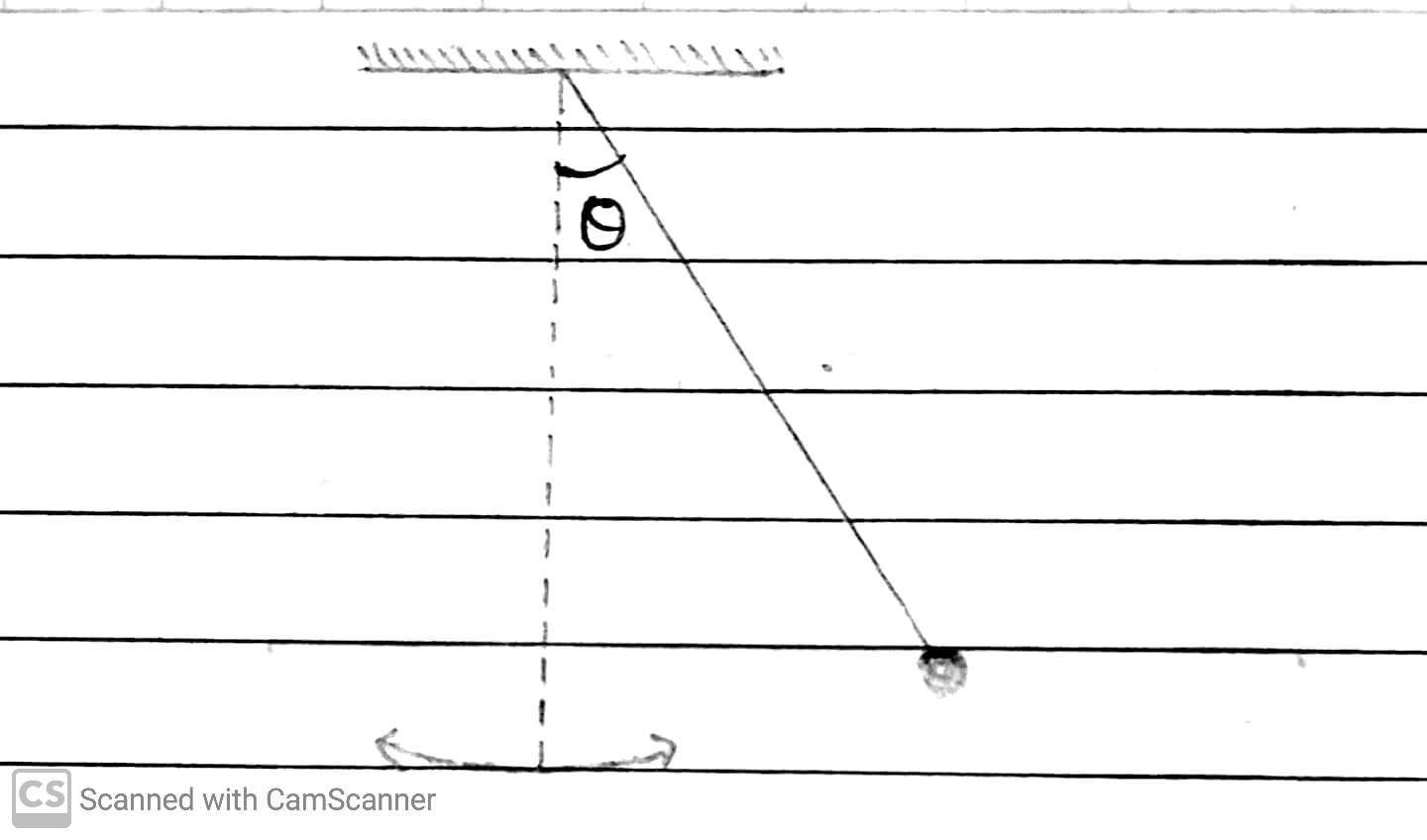
(II) In a simple pendulum, the displacement variable is its angular deviation(θ) from the vertical during oscillations with time.
Periodic Function
The displacement can be represented by a mathematical function of time the function which repeat its value in regular interval of time or period is called periodic function.
One of the simplest periodic function is given by
f(t) = A Cosωt
The time period for this function will be T = 2π/ω, because when we add 2π with the argument ωt of the function, then its value remain same.
Thus, the function f(t) is periodic with time T, then
f(t) = f(t+T)
The same result is correct if we consider a sine function, f(t) = A Sinωt
Further, a linear combination of sine and cosine functions
f(t) = A Sinωt + B Cosωt – (I)
Is a periodic function with time period T.

The above is an important result given by the French mathematician Jean Baptiste Jose Fourier(1768-1830).
Any periodic function can be expressed as a superposition of sine and cosine function of different time periods with suitable coefficients.
