A special type of periodic motion in which a particle moves to and fro repeatedly about a mean position under the influence of a restoring force is known as a simple harmonic motion (SHM).
The restoring forces always directed toward the mean position and its magnitude at any instant is directly proportional to the displacement of the particle from its mean position at that instant.
As the restoring force is directed toward the mean position at any point in its oscillation, Thus displacement of a simple harmonic motion is always a sinusoidal function of time.
Equation Of SHM
Let a particle oscillating back and forth about the origin of an x-axis between the limit +A to -A.

This oscillatory motion of the particle is said to be SHM if the displacement x of the particle from the origin varies with the time as
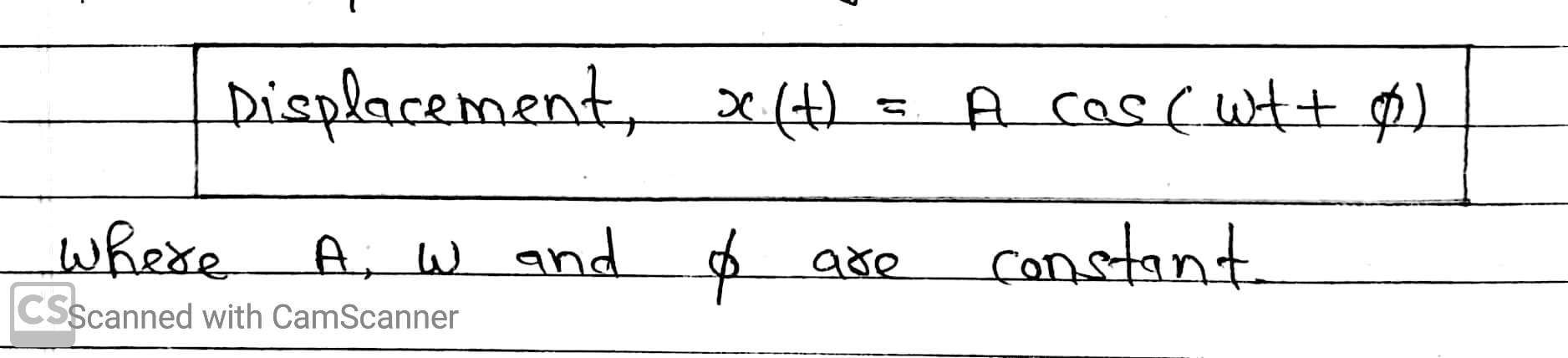
Let at any instant t, the particle be at P. If O is taken as mean position of the particle then OP=x

Where k is a force constant having SI unit N/m. The negative sign shows that the restoring force F is always directed towards the mean position.
The relation F=-kx is known as force law of SHM.
Location Of The Particle Executing SHM At The Discrete Value Of Time t
The below figure shows the positions of a particle executing SHM are discrete value of time. It must be noted that each interval of time being T/4.

Observations from the figures are as
(I) The time after which motion repeats itself is T.
(II) T will remain fixed i.e it does not very with variation in interval location (t=0).
(III) The speed is maximum for zero displacement at x=0 and Zero at the extremes of motion.
