Let a Fluid at rest having density ρ contained in a cylindrical vessel. Let the two point a and b separated by a vertical distance h.
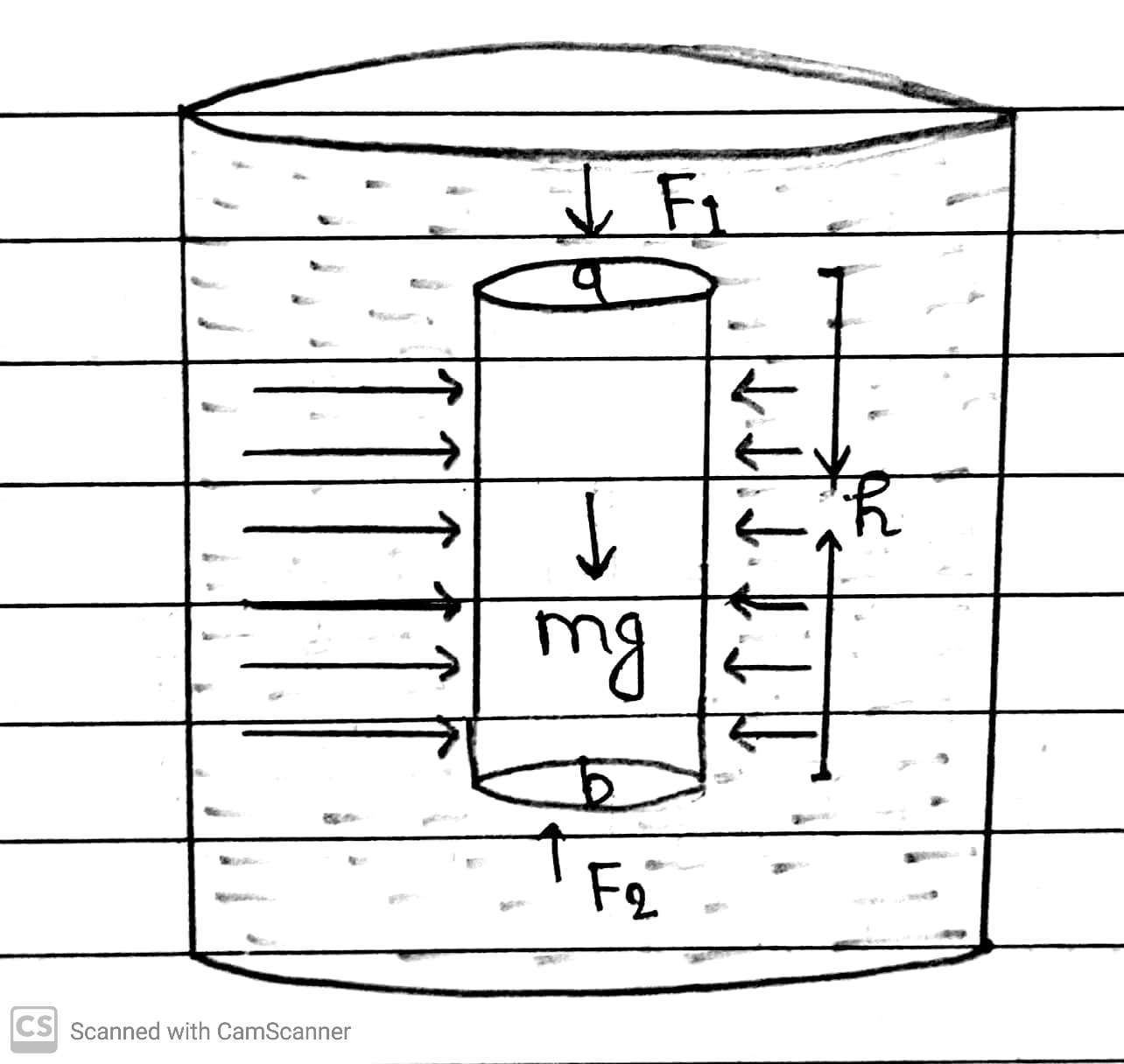
Now, we consider an imaginary cylinder of fluid of cross sectional area A, such that point a and b lie on its upper and lower circular faces respectively. Then weight of the fluid cylinder acting downwards,
W=mg = Volume × Density × g = Ahρg
[ mass = volume × density and V = Ah]
As the fluid is at rest the resultant horizontal forces should be zero and the resultant vertical forces should balance the weight of the element.

Hence, the pressure difference depends on the vertical height, density of the fluid and the acceleration due to gravity.
If point a is shifted to the fluid surface, which is open to the atmosphere, then we can replace P₁ by atmospheric pressure Pₐ and P₂ by P, then
Pressure, P = Pₐ+ρgh
This, the pressure P at depth below the surface of a liquid open to the atmosphere is greater than atmospheric pressure by an amount ρgh.
This excess of pressure at depth h in liquid P-Pₐ=ρgh is called gauge pressure at point b, while point a is at the liquid surface.
