
Chapter-10: Circles
Que 1. Prove that the line segments joining the points of contact of two parallel tangents is a diameter of the circle.
Ans 1. Consider the circle with center at O
PQ & RS are two parallel tangents to it touching at A and B respectively.
Join OA and OB
Now OA perpendicular to OQ (∴ radius is perpendicular to tangent)
And OB perpendicular to RS
∴ OA ∥ OB
But OA and OB pass through O
∴ AB is straight line through center
∴ AB is a diameter
Que 2. O is the centre of the circle and BCD is a tangent to it at C. Prove that ∠BAC + ∠ACD = 90 0.

Ans 2. Given: In the above figure, O is the centre of the circle and BCD is tangent to it at C.
To prove: ∠BAC + ∠ACD = 90°
Proof: In ΔOAC
OA = OC [radii of same circle]
⇒ ∠OCA = ∠OAC [angles opposite to equal sides are equal]
⇒ ∠OCA = ∠BAC [1]
Also,
OC ⊥ BD [Tangent at any point on a circle is perpendicular to the radius through point of contact]
⇒ ∠OCD = 90°
⇒ ∠OCA + ∠ACD = 90°
⇒ ∠BAC + ∠ACD = 90° [From 1]
Hence Proved
Que 3. In the figure quadrilateral, ABCD is drawn to circumscribe a circle. Prove that AD+BC = AB + CD.
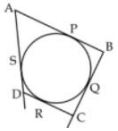
Ans 3. Given:- Let ABCD be the quadrilateral circumscribing the circle with centre O. The quadrilateral touches the circle at point P,Q,R and S.
To prove:- AB + CD + AD + BC
Proof:-
As we know that, length of tangents drawn from the external point are equal.
Therefore,
AP = AS…..(1)
BP = BQ…..(2)
CR = CQ…..(3)
DR = DS…..(4)
Adding equation (1),(2),(3) and (4), we get
AP + BP + CR + DR = AS = BQ + CQ + DS
(AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
⇒ AB + CD = AD + BC
Hence proved.
Que 4. Prove that the tangents drawn at the end-points of the diameter of a circle are parallel.
Ans 4. To prove: PQ ∣∣ RS
Given: A circle with centre O and diameter AB. Let PQ be the tangent at point A & Rs be the point B.
Proof: Since PQ is a tangent at point A.
OA ⊥ PQ(Tangent at any point of circle is perpendicular to the radius through point of contact).
∠OQP = 90o …………(1)
OB ⊥ RS
∠OBS = 90o ……………(2)
From (1) & (2)
∠OAP = ∠OBS
i.e., ∠BAP = ∠ABS
for lines PQ & RS and transversal AB
∠BAP = ∠ABS i.e., both alternate angles are equal.
So, lines are parallel.
therefore PQ || RS.
Que 5. Two concentric circles have centre O, OP = 4cm, OB = 5cm. AB is a chord of the outer circle and tangent to the inner circle at P. Find the length of AB.
Ans 5.

OP = 4 cm, OB = 5 cm
We know that the radius is perpendicular to the tangent at the point of contact.
∠OPB = 90o
In right triangle OPB,
OB2 = OP2 + PB2
(5)2 = (4)2 + PB2
PB2 = 25 – 16 = 9
PB = 3 cm
We know that perpendicular from the centre to the chord bisect the chord.

AB = 2PB = 6 cm
Que 6. Two tangents PA and PB are drawn to a circle with centre O such that ∠APB=120o. Prove that OP = 2AP
Ans 6. O is the center of the given circle
∠OAP = ∠OBP = 90o
(Radius is perpendicular to the tangent at the point of contact)
OA = OB
(radius of the circle)
∴ △OAP is congruent to △OBP
So that,
∠OPA = ∠OPB = 120/2 = 60o
In △OAP
cos∠OPA = cos60o = AP/OP {cos60o = 1/2}
1/2 = AP/OP
OP = 2AP Hence proved

Que 7. In the isosceles triangle ABC in fig. AB = AC, show that BF = FC.

Ans 7. ABC is an isosceles triangle (given) AB = AC (given) BE and CF are two medians (given) To prove: BE = CF In △CFB and △BEC CE = BF (Since, AC = AB = AC/2 = AB/2 = CE = BF) BC = BC (Common) ∠ECB = ∠FBC (Angle opposite to equal sides are equal) By SAS theorem: △CFB ≅ △BEC So, BE = CF (By c.p.c.t)
Que 8. In the fig. a circle is inscribed in a ∆ABC with sides AB = 12cm, BC = 8 cmand AC=10cm. Find the lengths of AD, BE and CF.

Ans 8. We know that AD = AF
BD = BE
CE = CF
Let AD = AF = x
BD = BE = y
CE = CF = z
Then x + y = 12
y + z = 8
x + z = 10
On Solving above equation we get x = 7,y = 5,z = 3
So AD = 7 , BE = 5 , CF = 3
Que 9. In fig. circle is inscribed in a quadrilateral ABCD in which ∠B = 90o. If AD = 23cm, AB = 29cm, and DS = 5cm, find the radius ‘r’ of the circle.

Ans 9. In the figure. AB, BC, CD and DA are the tangents drawn to the circle at Q, P, S and R respectively.
∴ DS = DR (tangents drawn from a external point D to the circle).
but DS = 5 cm (given)
∴ DR = 5 cm
In the fig. AD = 23 cm, (given)
∴ AR = AD – DR = 23 – 5 = 18 cm
but AR = AQ
(tangents drawn from an external point A to the circle)
∴ AQ = 18 cm
If AQ = 18 cm then (given AB = 29 cm)
BQ = AB – AQ = 29 – 18 = 11 cm
In quadrilateral BQOP,
BQ = BP (tangents drawn from an external point B)
OQ = OP (radii of the same circle)
∠QBP=∠QOP=90o (given)
∠OQB=∠OPB=90o (angle between the radius and tangent at the point of contact.)
∴ BQOP is a square.
∴ radius of the circle, OQ = 11 cm
Que 10. In fig. two circles touch each other externally at C. Prove that the common tangent at C bisects the other two tangents.

Ans 10. We know that lengths drawn from an external point to a
circle are equal
RP = RC and RC = RQ
RP = RQ
R is the mid-point of PQ.
RP – RO
R is the mid-point of PQ,
