Elastic Collision In Two Dimensions (Oblique Collision)

Let two body A and B of masses m₁ and m₂ kept on the x-axis. Initially the object B is at rest and A moves toward B with a speed u₁. If the collision is not head on, the object moves along different lines.

Let the object A moves with velocity v₁ making an angle θ with the x-axis and the object B moves with a velocity v₂ making an angle Ø with the same axis.

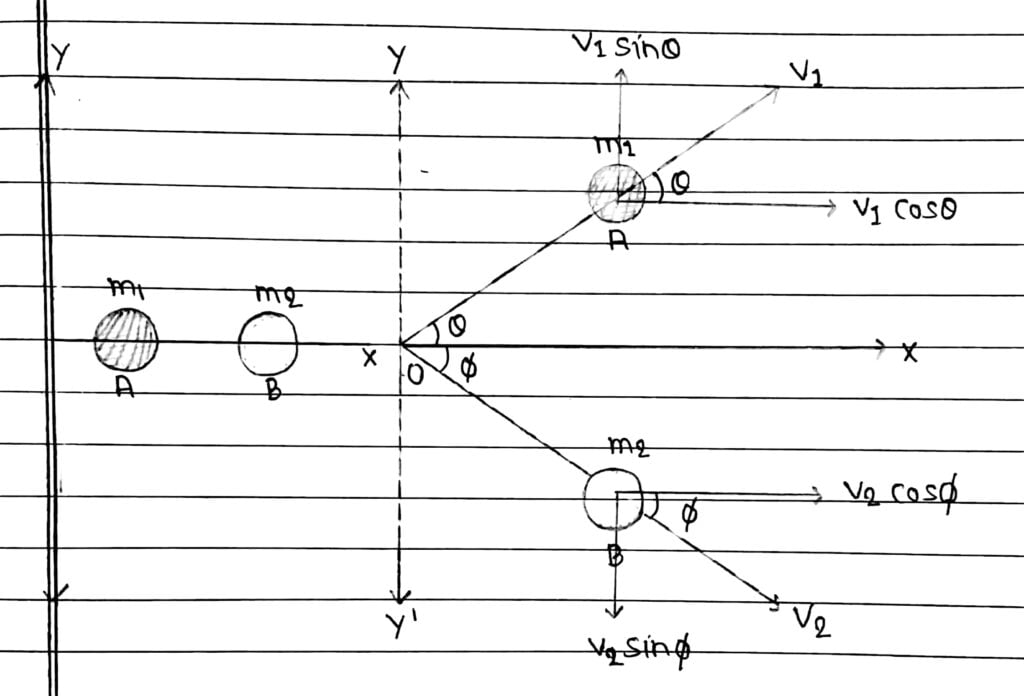
Elastic Collision In Two Dimensions (Oblique Collision)

Let v₁ and v₂ lie in xy-plane, then by using conservation of angular momentum in x and y direction, we get

In X-Direction

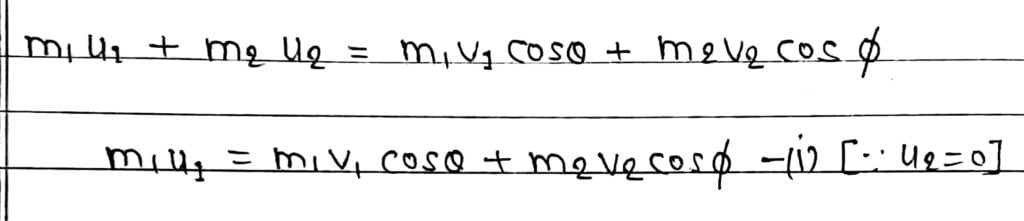
In Y-Direction

Initial momentum in y direction is zero, So

The four unknown quantities cannot be calculated by using the three equation, So if we calculate θ experimentally the value of other three unknown can be solved.

Now, The three casses can be considered as

Case-I:- Glancing Collision

In glancing collision, the incident partical does not lose any kinetic energy and is scattered almost undeflected. Thus for each collision θ is nearly equal to zero and Ø=90, then from equation (I) and (II), we get

u₁ = v₁ and v₂ = 0

Kinetic Energy of target particle = 1/2*m₂v₂² = 0

Case-II:- Head-On Collision

In this type of Collision, the target particle moves in the direction of the incident particle i.e Ø = 0, then from equation (I) and (II) becomes

m₁u₁ =m₁v₁cosθ + m₂v₂ and

0 = m₁v₁sinθ

From equation (III) the Kinetic Energy remains unchanged.

Case-III:- Elastic Collision Of Two Identical Particles

In this case,

Hence, We conclude that in a perfectly elastic collision, when a moving particle of mass m colloids elastically in two dimensions with another particle of mass m, after collision the two particle will move at right angle to each other.

NCERT Class 11 Physics Book PDF Free Download

In X-Direction

In Y-Direction

Case-I:- Glancing Collision

Case-II:- Head-On Collision

Case-III:- Elastic Collision Of Two Identical Particles

Also Read

NCERT Class 11 Physics Hand Written Notes Chapter-Wise

Related