The French scientist Blaise Pascal observed that pressure in a liquid at rest is the same at all point if they are at the same height. This is known as Pascal’s law.
Proof Of Pascal’s Law
It can be proved by using two principles as
- The force on any layer of a liquid at rest is normal to the layer.
- Newton’s first law of motion.
Now we consider an element in the interior of a fluid at rest. This element ABC-DEF is in the form of a right angled prism. This prismatic element is very small so that every part of it can be considered at the same depth from the liquid surface and therefore, the effect of the gravity is the same at all these points. The forces on this element are those exerted by the rest of the liquid and they must be normal to the surface of the element.
Let the fluid exert pressures Pa, Pb and Pc on the phases BEFC, ADFC and ADEB respectively of this element and the corresponding normal forces on these forces are Fa, Fb and Fc.
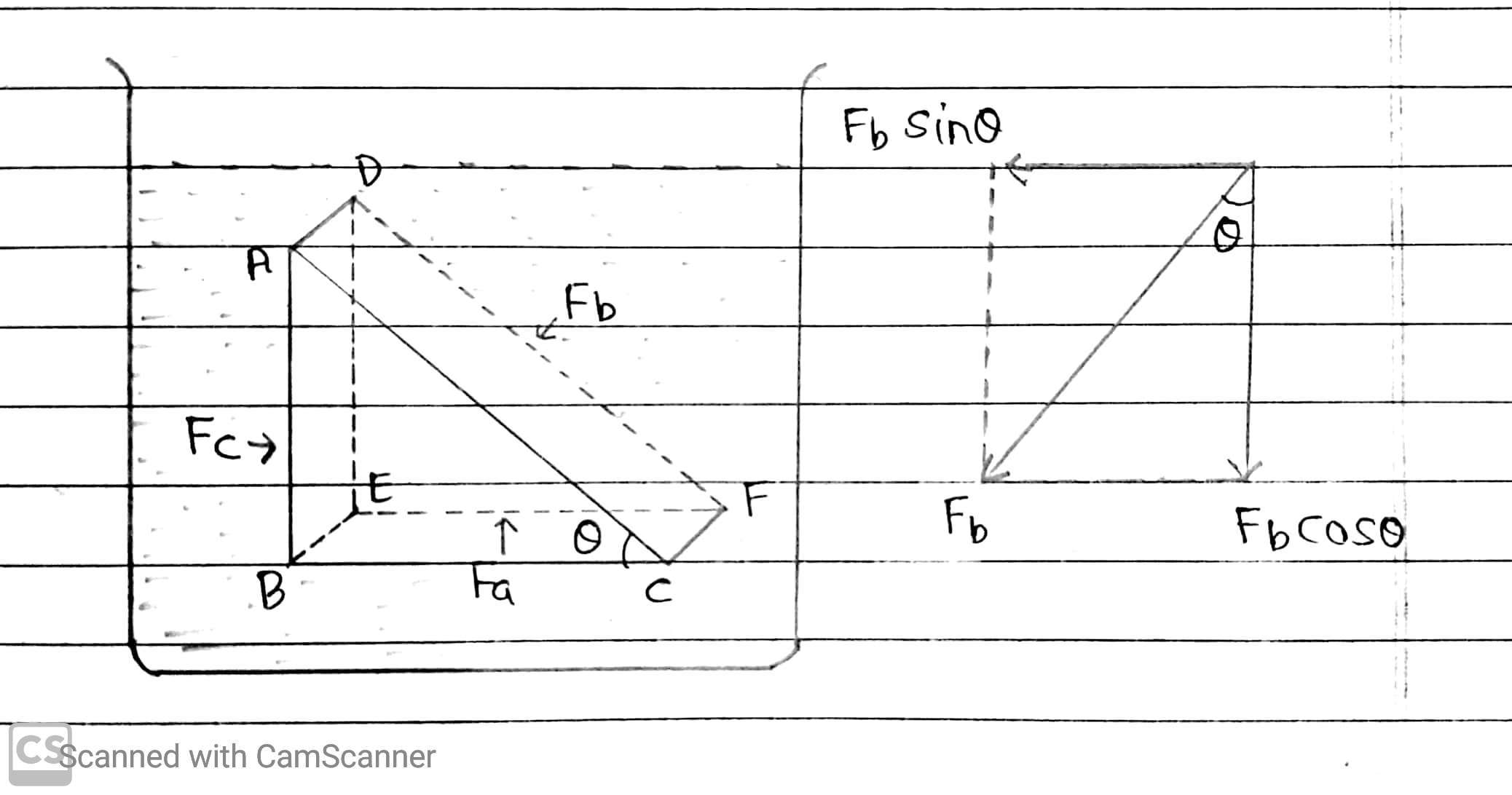
Let Aa, Ab and Ac be the respective areas of the three faces.


