This principle state that if only the conservative force are doing work on a body, then its total mechanical energy (kinetic energy + potential energy) remains constant.
Let a body undergoes displacement ∆x under the action of conservative force F(x), then from work energy theorem, the change in Kinetic Energy is
∆K = F(x).∆x (I)
As the force is conservative the change in Potential energy is given by
∆U = Negative of work done = – F(x).∆x (II)
Combining the above two equations, We get

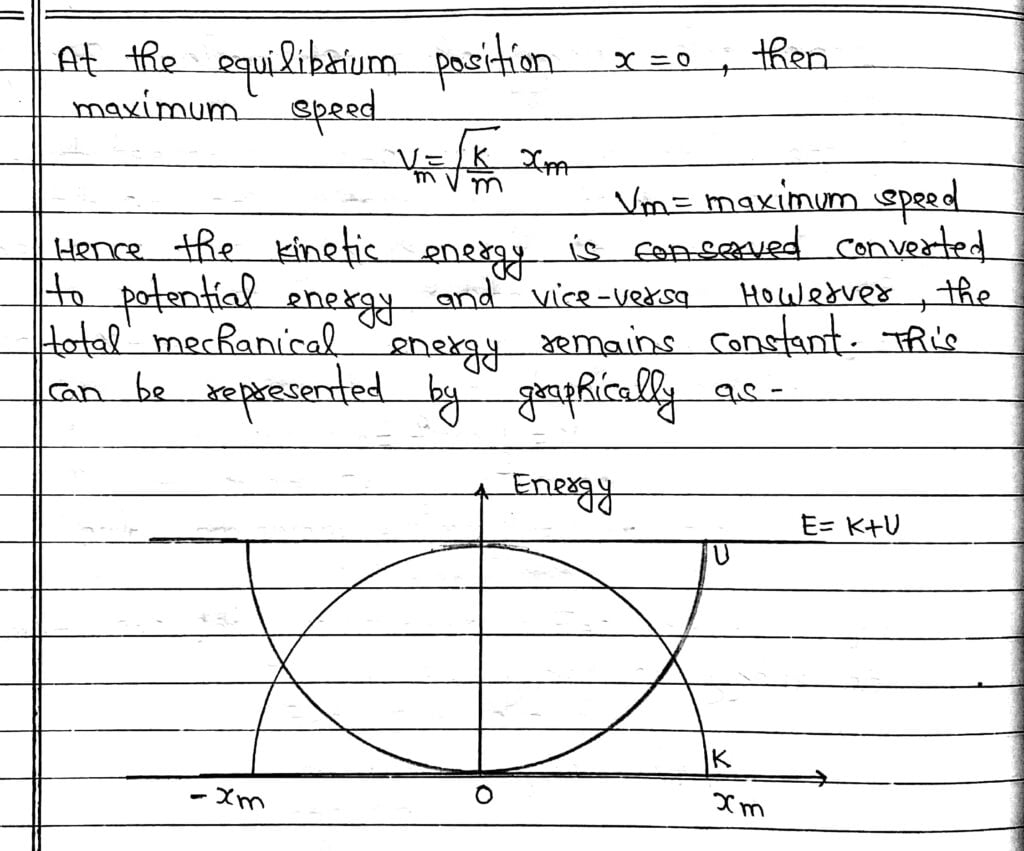
Although, individually the Kinetic Energy K and Potential Energy U may change from one state of the system to another, but their sum of the total Mechanical Energy of the system remains constant under the conservative force.
Mechanical Energy Of A Stretched Spring
If the block of mass m is extended to position Xm and released from rest, then it’s total Mechanical Energy at any arbitrary point X, where X is lies between – Xm and Xm.
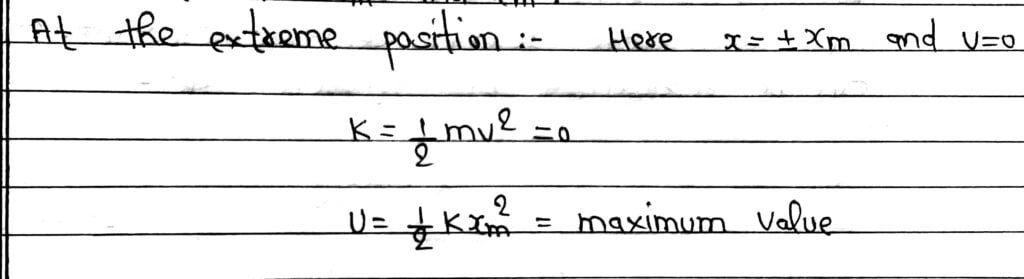
At any intermediate position X between -Xm and Xm, the energy is partially Kinetic Energy and Potential Energy.
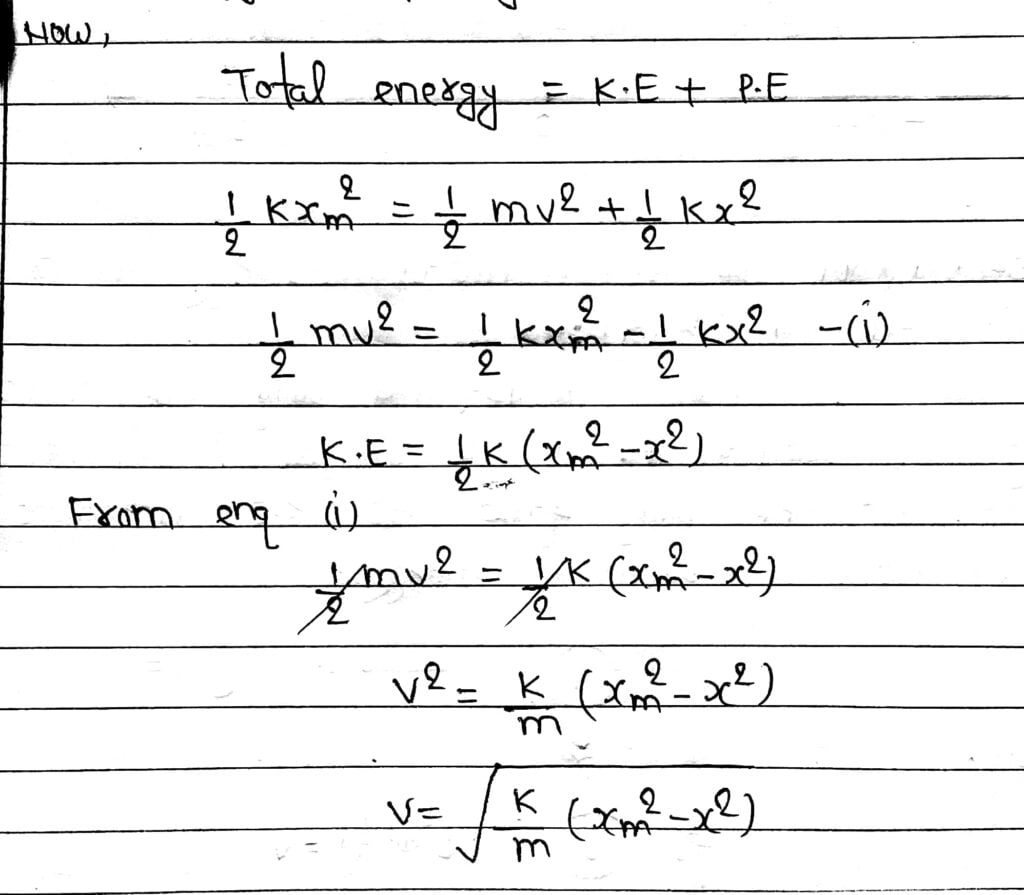
NCERT Class 11 Physics Book PDF Free Download
Also Read
SL Arora Class 11 Physics Book PDF Free Download
All In One Arihant Class 11 Physics Book PDF Free Download
Arihant All In One Chemistry Class 11 Book PDF Free Download
NCERT Class 11 Physics Hand Written Notes Chapter-Wise
Chapter-1 (Physical World) PDF Free Download
Chapter-2 (Units and Measurement) PDF Free Download
Chapter-3 (Motion In A Straight Line) PDF Free Download
Chapter-4 (Motion In A Plane) PDF Free Download
